Can I animate an object along a cosine curve?

Yes. Replace Math.sin() with Math.cos() to move the object along a cosine wave and adjust amplitude or frequency for variation.

Periodic Functions in C++ | Animate Sine and Cosine Waves

Understanding Periodic Functions | Maths Explanation for C++ Kids

In this tutorial, we'll learn how to use C++ periodic functions to create animations of sine and cosine waves. Understanding periodic functions is an essential part of senior secondary mathematics, and C++ offers a fun, visual way to explore them.

What Are Periodic Functions? | Maths Explanation for C++ Kids

A periodic function repeats its values at regular intervals. Common examples include the sine and cosine functions. In mathematics, these functions are essential for modeling waves and oscillations. In C++, we can easily simulate periodic functions like the sine and cosine curves using simple trigonometric equations. We'll represent these functions graphically using C++ Window Frame.

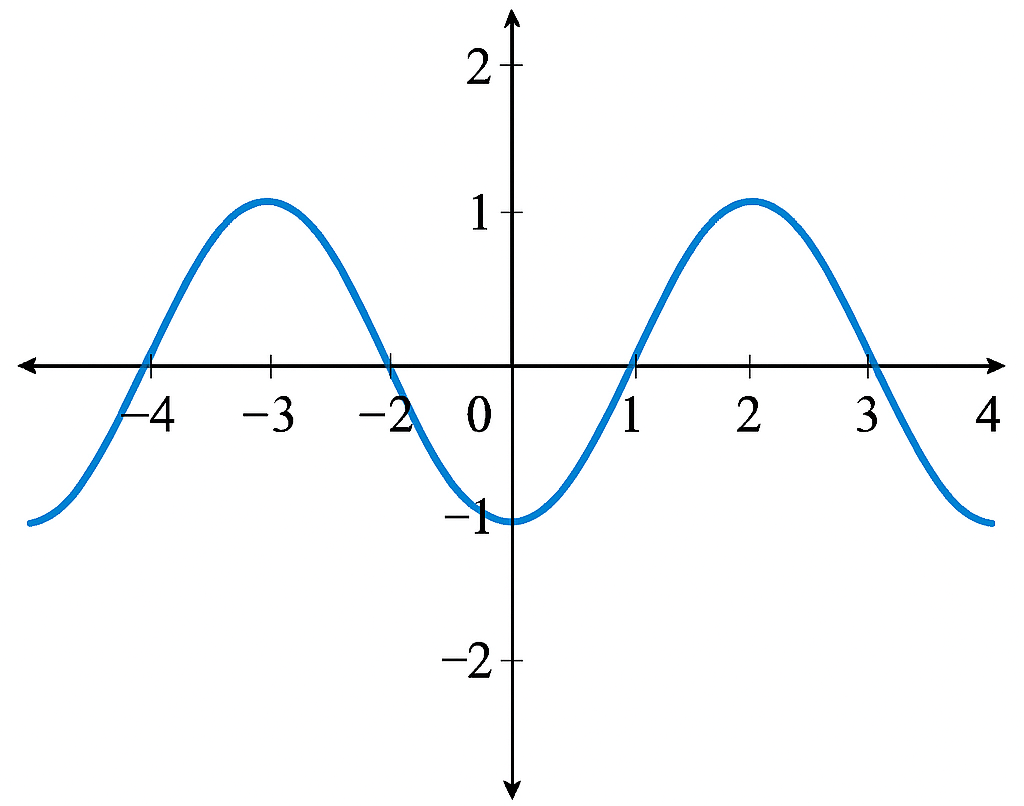
C++ periodic function cosine graph example — Figure 2: Graph of a periodic function showing cosine wave

Properties of Periodic Functions: Period, Amplitude & Frequency | Maths Explanation for C++ Kids

Every periodic function has three key properties:

Amplitude - the maximum height of the wave from its central position.
Period - the horizontal distance over which the function repeats.
Frequency - the number of complete cycles per unit interval.

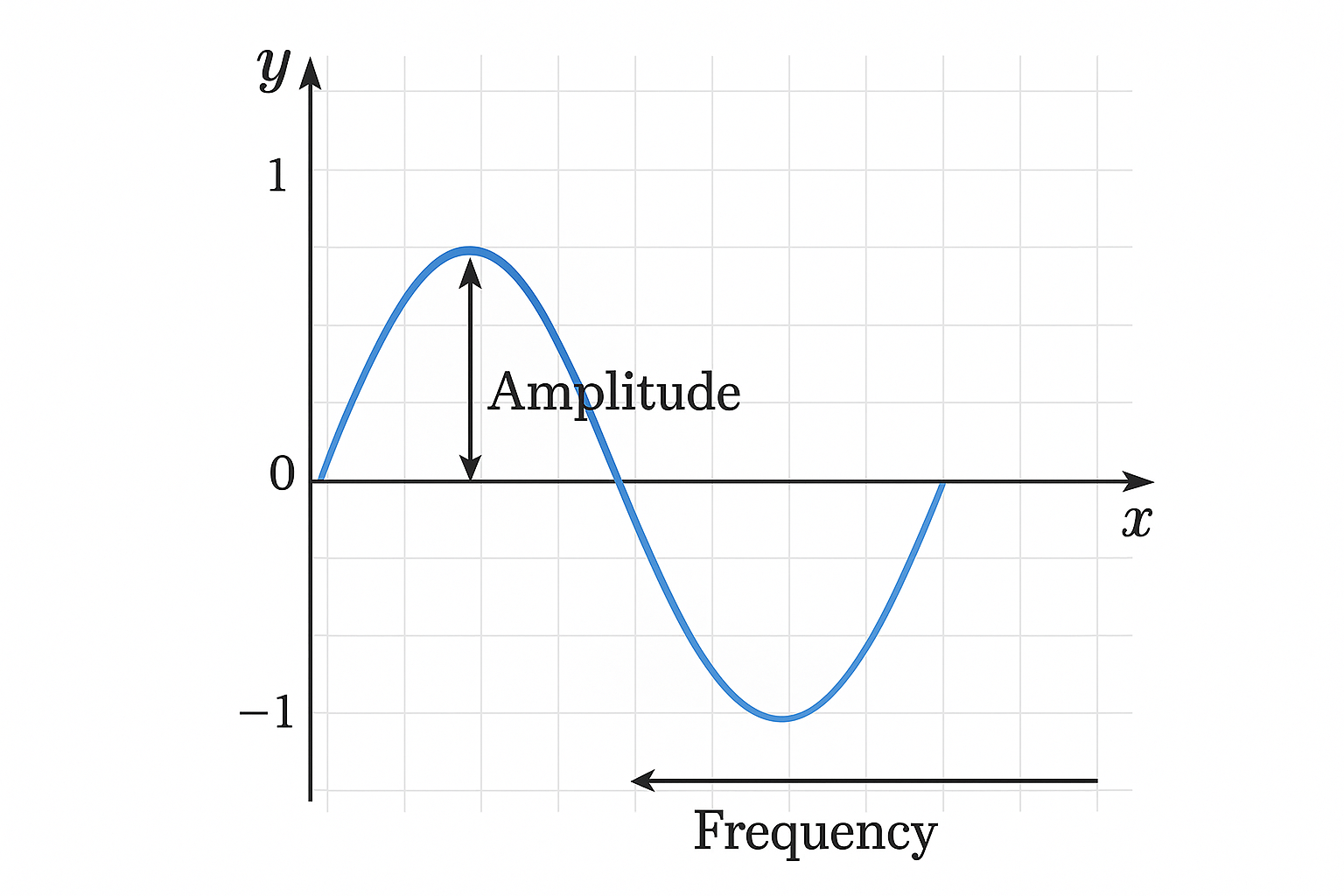
Graph of periodic function sine wave showing amplitude and frequency — Figure 1: Sine wave as an example of a periodic function

Understanding these properties helps in analyzing periodic function graphs and predicting their patterns.

How to Simulate Sinusoidal Curves in C++

Periodic functions produce an infinite order of sinusoidal curves.
The sine function has the general form y = a × sin(θ) + c;
and the cosine function has the general form y = a × cos(θ) + c;
where θ is angle in radians and a is an arbitrary constant that heightens the curve.

Animating a Periodic Wave Using C++

We can animate a sine or cosine wave in C++ using the C++ Window Frame. By incrementing θ continuously and computing y using the trigonometric function, a dot or object moves along a periodic path that represents the wave. The angle θ is in radians, and you can use any c value that gives a satisfactory amplitude.

Create a new C++ project; call it Dymetric.
Create 2 new C++ class files;
Call them Facet and PeriodicFunction.
Type out the adjoining C++ code for animating an image body through the path of a sine / cosine curve.
This code draws one complete periodic sine wave, allowing students to observe how the function repeats its pattern.

Exploring the Cosine Function in C++

Similar to the sine wave, we can animate the cosine curve using C++ trigonometric animation techniques.

Note: To create a cosine wave animation, simply replace Math.sin with Math.cos.

Key Takeaways on Periodic Wave Animation in C++

In this tutorial, you've learned:

Periodic functions repeat after a fixed interval called the period
They are fundamental in trigonometry, wave analysis, and C++ visualizations.
Use the C++ graphing example to explore amplitude, period, and phase shift interactively.

By blending mathematics and coding, students can better visualize abstract periodic concepts and prepare for advanced studies in both fields.

FAQs: Periodic Functions and C++

What is a periodic function in C++?

A periodic function repeats its values over intervals, such as sine or cosine, and can be represented graphically using C++ Window Frame and trigonometric functions.

How do you animate a sine wave using C++?

Use the Math.sin() function with the C++ Window Frame to simulate oscillations.

Can I animate objects along a periodic path in C++?

Yes! You can use sine and cosine to calculate x and y positions for smooth, looping motion.

Applications of Periodic Functions in C++ Programming and STEM Education

Periodic functions are used in physics, sound waves, and even game development. By coding these in C++, students can visualize maths periodic functions dynamically.

Understanding periodic functions in C++ helps students visualize mathematical concepts such as oscillation, waves, and harmonic motion. These concepts apply in fields like physics, sound processing, and even game development, where trigonometric animation brings realism to motion.

Summary: Periodic vs Aperiodic Functions | Maths Explanation for C++ Kids

Periodic functions in C++ are useful for simulating waves, oscillations, and rhythmic motion. Understanding the period, amplitude, and frequency of these functions helps you create dynamic visuals, animations, and simulations. Whether you're studying math periodic functions or applying them in web development, these tools make complex periodic behavior easier to model and visualize.

Not every function repeats itself.

A periodic function has a consistent cycle (e.g., sine, cosine).
An aperiodic function does not repeat (e.g., linear or exponential functions).

Understanding this difference helps students see why periodic motion is predictable - an important skill in physics, sound, and electrical circuits.

Mastering periodic functions prepares students for advanced trigonometry and real-life applications such as sound waves and electrical signals. Practice with our periodic function examples and questions to strengthen your understanding.

So! C++ Fun Practice Exercise - Animate along Periodic Wave

As a fun practice exercise, try modifying parameters like amplitude or frequency to explore how periodic functions in C++ behave. You can also:

Plot f(θ) = a * cos(θ) + c
Plot f(θ) = a * sin(2θ) + c
Write a C++ function that combines sine and cosine

This will be a great way to connect mathematics and programming, and help you understand more about C++ animations and periodic functions.

C++ Periodic Wave Dymetric Window Code Stub

Dymetric Header and Class Files

C++ Periodic Wave Canvas Frame and Button Controls - Header File

#pragma once

class Facet
{
public:
    Facet(HWND, int, int);
    virtual ~Facet();
    bool decorateButton(WPARAM, LPARAM);
    bool actionPerformed(HWND, WPARAM, LPARAM);
    void informPaint();
};

C++ Periodic Wave Canvas Frame and Button Controls - Class File

#include "stdafx.h"
#include "Facet.h"
#include "PeriodicFunction.h"

PeriodicFunction* pf_track;

/*
* Our custom class that interfaces between the parent window
* and the subsequent daemonstrator classes
*/
Facet::Facet(HWND hWnd, int window_width, int window_height)
{
    pf_track = new PeriodicFunction(hWnd, window_width, window_height);
}

/*
* This guy decorates buttons with colour and title text
*/
bool Facet::decorateButton(WPARAM wParam, LPARAM lParam) {
    // button glide calling
    if (wParam == 12321)
    {
        LPDRAWITEMSTRUCT lpDIS = (LPDRAWITEMSTRUCT)lParam;

        SetDCBrushColor(lpDIS->hDC, RGB(255, 192, 203));
        SelectObject(lpDIS->hDC, GetStockObject(DC_BRUSH));

        RECT rect = { 0 };
        rect.left = lpDIS->rcItem.left;
        rect.right = lpDIS->rcItem.right;
        rect.top = lpDIS->rcItem.top;
        rect.bottom = lpDIS->rcItem.bottom;

        RoundRect(lpDIS->hDC, rect.left, rect.top, rect.right, rect.bottom, 50, 50);
        // button text
        DrawText(lpDIS->hDC, TEXT("MOVE"), -1, &rect, DT_SINGLELINE | DT_CENTER | DT_VCENTER);

        return TRUE;
    }
    return FALSE;
}

/*
* Call the target class' draw method
*/
void Facet::informPaint() {
    pf_track->paint();
}

/*
* Say there is more than a single push button,
* this guy picks out the correct button that got clicked
* and calls the corresponding apt function
*/
bool Facet::actionPerformed(HWND hWnd, WPARAM wParam, LPARAM lParam)
{
    switch (LOWORD(wParam))
    {
    case 12321:
        pf_track->moveSinusoidal();
        return TRUE;
    default:
        return FALSE;
    }
}

Facet::~Facet()
{
    delete pf_track;
}

C++ Animation Code for Periodic Function - Header File

#pragma once

#define aWIDTH 10
#define aHEIGHT 10
#define PI 3.1415926535897932384626433832795

class PeriodicFunction
{
public:
    PeriodicFunction(HWND, int, int);
    virtual ~PeriodicFunction();
    void paint();
    void moveSinusoidal();
protected:
    HWND hWindow;
    HDC hdc;

    int window_width;
    int window_height;
    COLORREF ball_colour;
    int theta;
    int a; // constant
    int y;
    HPEN ball_pen;
    HBRUSH ball_brush;
};

C++ Animation Code for Periodic Function - Class File

#include "stdafx.h"
#include "PeriodicFunction.h"
#include <math.h>

PeriodicFunction::PeriodicFunction(HWND hWnd, int window_width, int window_height)
{
    hWindow = hWnd; // save away window handle
    this->window_width = window_width; // save away window width
    this->window_height = window_height; // save away window width

    ball_colour = RGB(255, 0, 0);
    theta = 0;
    a = 100; // constant

    // convert theta from degree to radians (work in a little translate for y)
    y = (int)round(a * sin(theta * (long double)PI / 180)) + int(window_height / 2);

    // Pen and brush for travelling ball
    ball_pen = CreatePen(PS_SOLID, 1, RGB(0, 0, 0));
    ball_brush = CreateSolidBrush(ball_colour);

    hdc = GetDC(hWindow);

    SelectObject(hdc, ball_pen); // select ball pen colour
    SelectObject(hdc, ball_brush); // select ball brush colour

    // draw a second demarcation line
    MoveToEx(hdc, 0, 80, NULL);
    LineTo(hdc, window_width, 80);

    // draw x-axis
    MoveToEx(hdc, 0, int(window_height/2 + aHEIGHT/2), NULL);
    LineTo(hdc, window_width, int(window_height/2 + aHEIGHT/2));
}

/*
* draws the ball/circle using the apt color
*/
void PeriodicFunction::paint() {
    // draw a dot
    Ellipse(hdc, theta, y, theta + aWIDTH, y + aHEIGHT);
}

void PeriodicFunction::moveSinusoidal() {
    // condition for continuing motion
    while (theta + aWIDTH < window_width) {
        // work in a little translate for y
        y = (int)round(a * sin(theta * (long double)PI / 180)) + int(window_height / 2);
        paint();

        theta += 15;
        // introduce a delay between renderings
        Sleep(50);
    }
}

PeriodicFunction::~PeriodicFunction()
{
    DeleteObject(ball_pen);
    DeleteObject(ball_brush);

    ReleaseDC(hWindow, hdc);
}

I have a better version / See other versions.