Can I animate an object along a cosine curve?

Yes. Replace Math.sin() with Math.cos() to move the object along a cosine wave and adjust amplitude or frequency for variation.

Periodic Functions in VB.Net | Animate Sine and Cosine Waves

Understanding Periodic Functions | Maths Explanation for VB.Net Kids

In this tutorial, we'll learn how to use VB.Net periodic functions to create animations of sine and cosine waves. Understanding periodic functions is an essential part of senior secondary mathematics, and VB.Net offers a fun, visual way to explore them.

What Are Periodic Functions? | Maths Explanation for VB.Net Kids

A periodic function repeats its values at regular intervals. Common examples include the sine and cosine functions. In mathematics, these functions are essential for modeling waves and oscillations. In VB.Net, we can easily simulate periodic functions like the sine and cosine curves using simple trigonometric equations. We'll represent these functions graphically using VB.Net Windows Form.

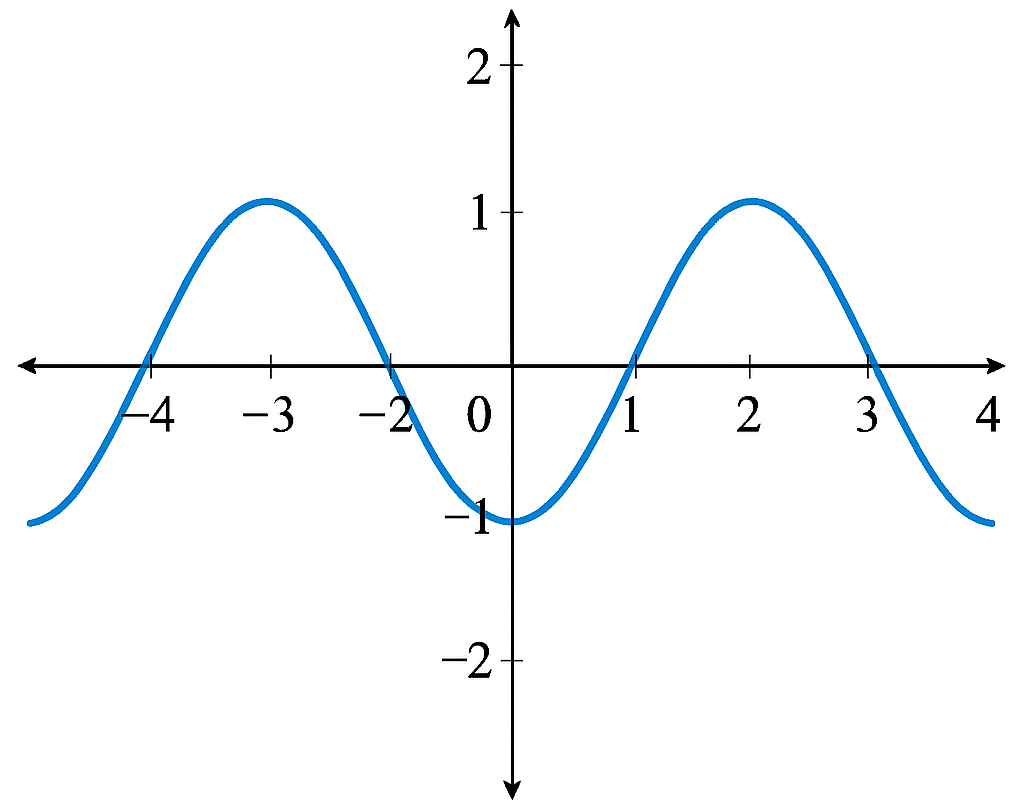
VB.Net periodic function cosine graph example — Figure 2: Graph of a periodic function showing cosine wave

Properties of Periodic Functions: Period, Amplitude & Frequency | Maths Explanation for VB.Net Kids

Every periodic function has three key properties:

Amplitude - the maximum height of the wave from its central position.
Period - the horizontal distance over which the function repeats.
Frequency - the number of complete cycles per unit interval.

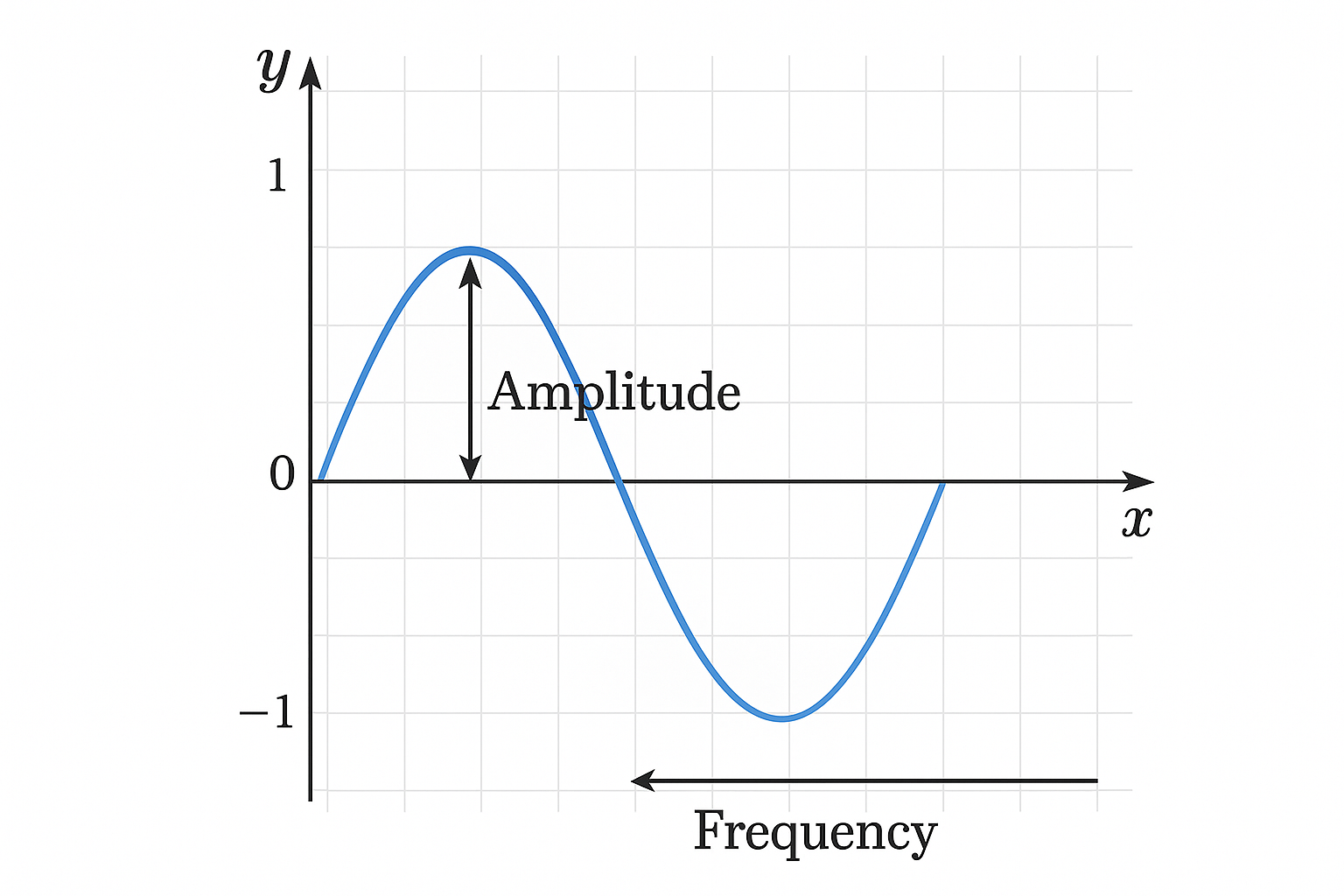
Graph of periodic function sine wave showing amplitude and frequency — Figure 1: Sine wave as an example of a periodic function

Understanding these properties helps in analyzing periodic function graphs and predicting their patterns.

How to Simulate Sinusoidal Curves in VB.Net

Periodic functions produce an infinite order of sinusoidal curves.
The sine function has the general form y = a × sin(θ) + c;
and the cosine function has the general form y = a × cos(θ) + c;
where θ is angle in radians and a is an arbitrary constant that heightens the curve.

Animating a Periodic Wave Using VB.Net

We can animate a sine or cosine wave in VB.Net using the VB.Net Windows Form. By incrementing θ continuously and computing y using the trigonometric function, a dot or object moves along a periodic path that represents the wave. The angle θ is in radians, and you can use any c value that gives a satisfactory amplitude.

Create a new Visual Basic Windows Forms Application project ; call it Dymetric_VB.
Create 3 new VB.Net classes;
Call them Facet, Dymetric and PeriodicFunction.
Type out the adjoining VB.Net code for animating an image body through the path of a sine / cosine curve.
This code draws one complete periodic sine wave, allowing students to observe how the function repeats its pattern.

Exploring the Cosine Function in VB.Net

Similar to the sine wave, we can animate the cosine curve using VB.Net trigonometric animation techniques.

Note: To create a cosine wave animation, simply replace Math.sin with Math.cos.

Key Takeaways on Periodic Wave Animation in VB.Net

In this tutorial, you've learned:

Periodic functions repeat after a fixed interval called the period
They are fundamental in trigonometry, wave analysis, and VB.Net visualizations.
Use the VB.Net graphing example to explore amplitude, period, and phase shift interactively.

By blending mathematics and coding, students can better visualize abstract periodic concepts and prepare for advanced studies in both fields.

FAQs: Periodic Functions and VB.Net

What is a periodic function in VB.Net?

A periodic function repeats its values over intervals, such as sine or cosine, and can be represented graphically using VB.Net Windows Form and trigonometric functions.

How do you animate a sine wave using VB.Net?

Use the Math.sin() function with the VB.Net Windows Form to simulate oscillations.

Can I animate objects along a periodic path in VB.Net?

Yes! You can use sine and cosine to calculate x and y positions for smooth, looping motion.

Applications of Periodic Functions in VB.Net Programming and STEM Education

Periodic functions are used in physics, sound waves, and even game development. By coding these in VB.Net, students can visualize maths periodic functions dynamically.

Understanding periodic functions in VB.Net helps students visualize mathematical concepts such as oscillation, waves, and harmonic motion. These concepts apply in fields like physics, sound processing, and even game development, where trigonometric animation brings realism to motion.

Summary: Periodic vs Aperiodic Functions | Maths Explanation for VB.Net Kids

Periodic functions in VB.Net are useful for simulating waves, oscillations, and rhythmic motion. Understanding the period, amplitude, and frequency of these functions helps you create dynamic visuals, animations, and simulations. Whether you're studying math periodic functions or applying them in web development, these tools make complex periodic behavior easier to model and visualize.

Not every function repeats itself.

A periodic function has a consistent cycle (e.g., sine, cosine).
An aperiodic function does not repeat (e.g., linear or exponential functions).

Understanding this difference helps students see why periodic motion is predictable - an important skill in physics, sound, and electrical circuits.

Mastering periodic functions prepares students for advanced trigonometry and real-life applications such as sound waves and electrical signals. Practice with our periodic function examples and questions to strengthen your understanding.

So! VB.Net Fun Practice Exercise - Animate along Periodic Wave

As a fun practice exercise, try modifying parameters like amplitude or frequency to explore how periodic functions in VB.Net behave. You can also:

Plot f(θ) = a * cos(θ) + c
Plot f(θ) = a * sin(2θ) + c
Write a VB.Net function that combines sine and cosine

This will be a great way to connect mathematics and programming, and help you understand more about VB.Net animations and periodic functions.

VB.Net Periodic Wave Window Display Code Stub

Public Class Form1

    Private form_details As New Facet
    Private action_class As New Dymetric

    Private Sub Form1_Load(sender As Object, e As EventArgs) Handles MyBase.Load
        ' Fill in Form - Put button on form
        form_details.formFeatures(sender)
    End Sub

    Private Sub Form1_Paint(sender As Object, e As PaintEventArgs) Handles Me.Paint
        ' Colour button area
        form_details.decorateButtonArea(sender, e)

        ' Call MovingBody class into action
        action_class.decideAction(sender, Me.CreateGraphics(), form_details.CLICK_OCCURRED)

        ' Reset click variable
        form_details.CLICK_OCCURRED = False
    End Sub
End Class

VB.Net Periodic Wave Facet Window Code Stub

Public Class Facet

    Dim screen_rect As Rectangle
    Public CLICK_OCCURRED As Boolean = False

    Public Sub formFeatures(sender As Object)
        'Set window position, width and height
        screen_rect = Screen.PrimaryScreen.Bounds
        sender.SetDesktopBounds(0, 0, screen_rect.Width, screen_rect.Height)

        ' Set a display text
        sender.Text = "useOfMaths.com"

        ' Set a background colour
        sender.BackColor = System.Drawing.Color.LightGray

        ' Set an icon image
        Dim path = System.IO.Path.GetDirectoryName(System.Reflection.Assembly.GetExecutingAssembly().CodeBase)
        path = New Uri(path).LocalPath
        Try
            sender.Icon = New Icon(path & "\useOfMaths.ico")
        Catch ex As System.IO.FileNotFoundException
            ' Well, just go on and use default pic
        End Try

        '
        'create a button - response_btn
        '
        Dim response_btn As New Button()
        response_btn.BackColor = System.Drawing.Color.Magenta
        response_btn.ForeColor = System.Drawing.Color.Blue
        response_btn.Name = "response_btn"
        response_btn.SetBounds(CInt(Math.Round(screen_rect.Width / 2)) - 50, 5, 100, 40)
        response_btn.Text = "Move"
        sender.Controls.Add(response_btn)
        AddHandler response_btn.Click, AddressOf response_btn_Click
    End Sub

    Public Sub decorateButtonArea(sender As Object, e As PaintEventArgs)
        ' Draw a dotted line
        Dim pencil As New System.Drawing.Pen(System.Drawing.Color.Black)
        pencil.DashStyle = Drawing2D.DashStyle.DashDot
        pencil.Width = 5
        e.Graphics.DrawLine(pencil, 0, 50, sender.Width, 50)
        pencil.Dispose()

        ' Colour region
        Dim paint_brush As New System.Drawing.SolidBrush(System.Drawing.Color.Pink)
        e.Graphics.FillRectangle(paint_brush, 0, 0, sender.Width, 50)
        paint_brush.Dispose()
    End Sub

    Public Sub response_btn_Click(sender As Object, e As EventArgs)
        ' turn this on on every button click
        CLICK_OCCURRED = True
        sender.Refresh()
    End Sub
End Class

VB.Net Periodic Wave Code for Dymetric Class

Public Class Dymetric
    Private sine_curve As New PeriodicFunction
    Private do_simulation = False

    ' decide what course of action to take
    Public Sub decideAction(sender As Object, g As Graphics, click_check As Boolean)
        If do_simulation And click_check Then
            ' do animation
            sine_curve.play(sender, g)
            do_simulation = False
        Else
            ' Put ball on screen
            sine_curve.prep(sender, g)
            do_simulation = True
        End If
    End Sub
End Class

VB.Net Animation Code for Periodic Function class

Public Class PeriodicFunction

    Private theta, a, y, half_vert_screen As Integer
    Private Const dotDIAMETER = 10

    Dim dot_colour As New System.Drawing.SolidBrush(System.Drawing.Color.Yellow)
    Dim bg_colour As New System.Drawing.SolidBrush(System.Drawing.Color.LightGray)

    ' draw first appearance of dot on the screen
    Public Sub prep(sender As Object, g As Graphics)
        theta = 0
        a = sender.Height / 3 ' constant
        ' half way down the vertical section of the screen
        half_vert_screen = sender.Height / 2
        y = CInt(Math.Round(a * Math.Sin(theta * Math.PI / 180)) + half_vert_screen)

        ' clear entire used canvas area
        g.FillRectangle(bg_colour, 0, 60, sender.Width, sender.Height)
        ' draw x-axis line
        g.DrawLine(Pens.Black, 0, half_vert_screen + 5, sender.Width, half_vert_screen + 5)
        ' draw dot
        g.FillEllipse(dot_colour, theta, y, dotDIAMETER, dotDIAMETER)
    End Sub

    ' repetitively clear and draw dot on the screen - Simulate motion
    Public Sub play(sender As Object, g As Graphics)
        ' condition for continuing motion
        Do While theta < sender.Width - dotDIAMETER
            y = CInt(Math.Round(a * Math.Sin(theta * Math.PI / 180)) + half_vert_screen)

            ' redraw dot
            g.FillEllipse(dot_colour, theta, y, dotDIAMETER, dotDIAMETER)

            theta += 15
            ' take a time pause
            Threading.Thread.Sleep(50)
        Loop
    End Sub
End Class

I have a better version / See other versions.