Combination in C#

Code for Doing Combination in C#

Writing up an algorithm to carry out the different Combination - Selection without Repetition, ⁿC_r - of a set of things in C# requires some level of imaginative thinking.

Get a writing pad and pencil:

Write out all n members in the set - for Combination - at the top of the pad.
Beginning with the first member, match it separately with the other members until the required selected-group size (r) is reached.
When every possible Combination for this first member is exhausted, remove the current first member from the mother set.
The immediate next member becomes the new first member in the culminating set.
Take the first member in what is left of the mother set and repeat the same process from step II.

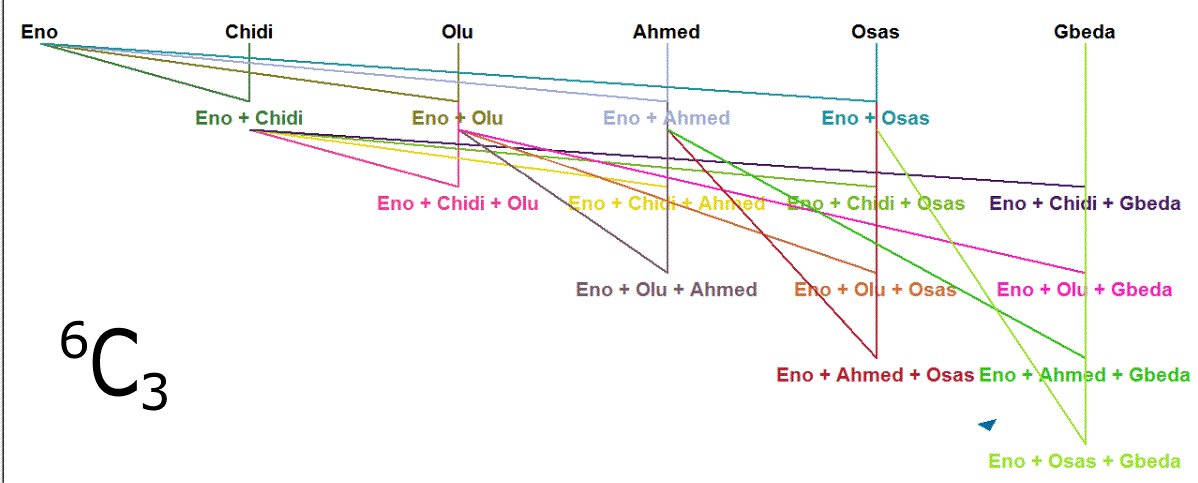
This is exactly what we will do with code to list up all possible selections without repetition in C#.

Create a new C# project; call it Miscellaneous_CS.
Create a new C# class file; call it Combination.

Type out the adjoining C# code for the combination of different options (ⁿC_r).

Why Bother About Combination

Well, isn't it obvious?
Say you are to pick only four (4) pupils from a class of six - such a small class; our little Combination algorithm solves this little problem for you by showing all your possible options / selection outcomes.

C# code for Combination Class

using System.Collections.Generic;

namespace Miscellaneous
{
    class Combination
    {
        public List<string> words;
        public int r; // min length of word
        protected List<string[]> comb_store;
        private int i;

        public Combination()
        {
        }

        // point of entry
        public List<string[]> possibleWordCombinations(List<string> candidates, int size) {
            words = candidates;
            r = size;
            comb_store = new List<string[]>();
            i = 0;
            // check for conformity
            if (r <= 0 || r > words.Count) {
                comb_store = new List<string[]>();
            }
            else if (r == 1) {
                for (; i < words.Count; i++) {
                    comb_store.Add(new string[] { words[i] });
                }
            }
            else {
                progressiveCombination();
            }
            return comb_store;
        }

        // do combinations for all 'words' element
        private void progressiveCombination() {
            //                  single member list
            repetitivePairing(new List<string>() {words[i]}, i + 1);
            if (i + r <= words.Count) {
                // move on to next degree
                i++;
                progressiveCombination();
            }
        }

        // do all possible combinations for 1st element of this array
        private void repetitivePairing(List<string> prefix, int position) {
            List<string>[] auxiliary_store = new List<string>[words.Count - position];
            for (int j = 0; position < words.Count; position++, j++) {
                // check if desired -- r -- size will be realised
                if (r - prefix.Count <= words.Count - position) {
                    auxiliary_store[j] = new List<string>();
                    auxiliary_store[j].AddRange(prefix);
                    auxiliary_store[j].Add(words[position]);
                    if (auxiliary_store[j].Count < r) {
                        // see to adding next word on
                        repetitivePairing(auxiliary_store[j], position + 1);
                    }
                    else {
                        comb_store.Add(auxiliary_store[j].ToArray());
                    }
                }
            }
        }
    }
}

Main Class

using System;
using System.Collections.Generic;

namespace Miscellaneous
{
    class Program
    {
        static void Main(string[] args)
        {
            List<string> goods;
            goods = new List<string>() { "Eno", "Chidi", "Olu", "Ahmed", "Osas", "Gbeda" };
            Combination combo = new Combination();
            List<string[]> result = combo.possibleWordCombinations(goods, 3);
            // print choices and operation
            Console.Write("[ ");
            foreach (string choice in combo.words)
            {
                Console.Write(choice + "; ");
            }
            Console.WriteLine("] combination " + combo.r + ":" + Environment.NewLine);
            // print out combinations nicely
            int i = 0;
            foreach (string[] set in result)
            {
                Console.Write(++i + ": ");
                foreach (string member in set)
                {
                    Console.Write(member + "; ");
                }
                Console.WriteLine();
            }
            Console.WriteLine(Environment.NewLine + "Number of ways is " + result.Count + ".");
        }
    }
}

I have a better version / See other versions.