usingMaths.com
From Theory to Practice - Math You Can Use.







<< PreviousNext >>

Code for Combination (Selection Without Repetition) in Python



Code for Doing Combination in Python

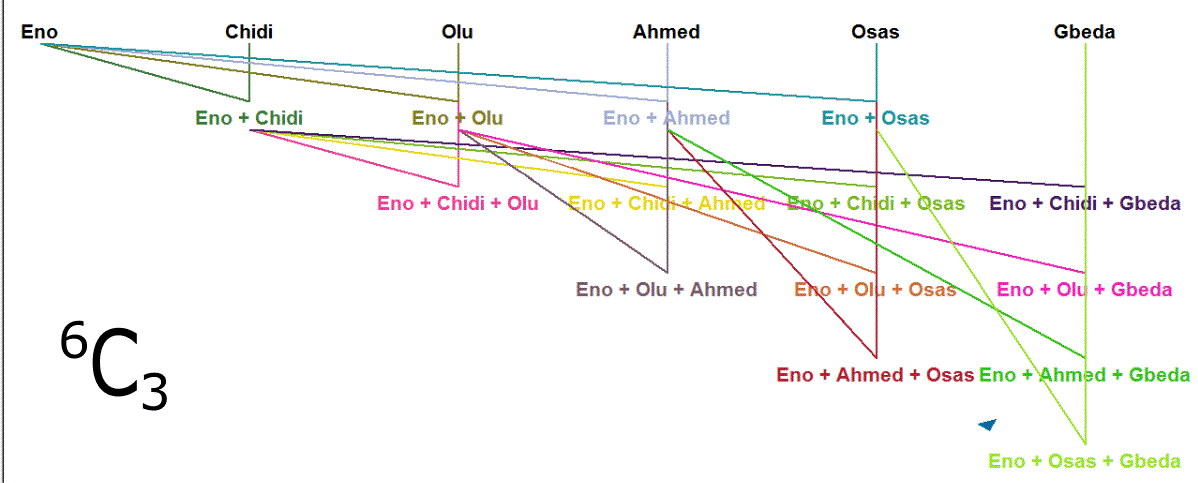
Writing up an algorithm to carry out the different Combination - Selection without Repetition, nCr - of a set of things in Python requires some level of imaginative thinking.

Get a writing pad and pencil:
  1. Write out all n members in the set - for Combination - at the top of the pad.
  2. Beginning with the first member, match it separately with the other members until the required selected-group size (r) is reached.
  3. When every possible Combination for this first member is exhausted, remove the current first member from the mother set.
    The immediate next member becomes the new first member in the culminating set.
  4. Take the first member in what is left of the mother set and repeat the same process from step II.

How to carry out combination

This is exactly what we will do with code to list up all possible selections without repetition in Python.

Create a new Python Class File; call it Miscellaneous.py.
Create a new Python Module File; call it Combination.py.

Type out the adjoining Python code for the combination of different options (nCr).


Why Bother About Combination

Well, isn't it obvious?
Say you are to pick only four (4) pupils from a class of six - such a small class; our little Combination algorithm solves this little problem for you by showing all your possible options / selection outcomes.







Python Code for Combination.py Module

# Sure enough this is a module

# define a class
class Combinatorial:

    def __init__(self):
        self.i = 0

    # point of entry
    def possibleWordCombinations(self, candidates, size):
        self.words = candidates
        self.r = size
        self.comb_store = [] 
        self.i = 0
        # check for conformity
        if self.r <= 0 or self.r > len(self.words):
            self.comb_store = ()
        elif self.r == 1:
            for word in self.words:
                self.comb_store.append((word))
        else:
            self.progressiveCombination()

        return self.comb_store


    # do combinations for all 'words' element
    def progressiveCombination(self):
        #            single member list
        self.repetitivePairing([self.words[self.i]], self.i + 1)
        if self.i + self.r <= len(self.words):
            # move on to next degree
            self.i += 1
            self.progressiveCombination()

    # do all possible combinations for 1st element of this array
    def repetitivePairing(self, prefix, position):
        auxiliary_store = [[] for k in range(len(self.words) - position)]
        for j in range(len(self.words) - position):
            # check if desired -- r -- size will be realised
            if j + self.i + self.r <= len(self.words):
                auxiliary_store[j].extend(prefix)
                auxiliary_store[j].append(self.words[position])
                if len(auxiliary_store[j]) < self.r:
                    # see to adding next word on
                    self.repetitivePairing(auxiliary_store[j], position + 1)
                else:
                    self.comb_store.append(tuple(auxiliary_store[j]))
            position += 1

Main Class

#!/usr/bin/python

from Combination import Combinatorial

# Use the combination module/class
goods = ["Eno", "Chidi", "Olu", "Ahmed", "Osas", "Gbeda"]

combo = Combinatorial()
result = combo.possibleWordCombinations(goods, 3)

# print choices and operation
print("\n", combo.words, " combination ", combo.r, ":\n")

# print out combinations nicely
i = 0
for group in result:
    i += 1
    print(i, ": ", group)
    
print("\n\nNumber of ways is ", len(result), ".\n")



<< PreviousNext >>