Introduction to Combinations (\(^nC_r\)) in Java
Combinatorics is a key area of mathematics and computer science, and one of its most common applications is calculating combinations. In this tutorial, you'll learn how to implement a Java combination algorithm to calculate \(^nC_r\) in Java. We'll explore how to generate all possible selections without repetition, compare combinations with permutations, and walk through practical coding examples.
What Is a Combination? | Mathematics Explanation for Java Kids
A combination is a way of selecting items from a group where order does not matter. For example, choosing 3 students out of a class of 10 is a combination problem. In Java, we can write functions to calculate these selections efficiently.
A combination answers the question: “In how many different ways can r items be chosen from n items when order is irrelevant?” For example, choosing {A, B} is the same as choosing {B, A}. Because the order does not matter, combinations differ from permutations.
Combinations are commonly used in:
- Probability calculations
- Statistical analysis
- Algorithmic problem solving
- Data sampling and modeling
Understanding how combinations work mathematically makes it easier to implement them correctly in programming languages such as Java.
Combination Formula (\(^nC_r\)) Explained
The standard formula for combinations is written as \(^nC_r\) and defined as:
- n is the total number of items
- r is the number of items selected
- ! denotes factorial
This formula computes the number of possible selections without repetition and without regard to order.
Combinations vs. Permutations | Maths Explanation for Java Kids
It is easy to confuse these two concepts. Remember:
- Combination: Choosing a team of 3 students from a class of 20 (Order doesn't matter).
- Permutation: Assigning a President, VP, and Secretary from a class of 20 (Order matters).
This page is specifically designed for selection without repetition, the standard definition of the combination formula.
Selection Without Repetition Using Java
In selection without repetition, once an item is chosen, it cannot be chosen again. This assumption is built directly into the combination formula and is reflected in the Java implementation above.
This type of algorithm is commonly used when:
- Selecting unique samples from a dataset
- Solving probability problems
- Analyzing possible outcomes in simulations
- Teaching foundational combinatorics concepts
The Java function that follows computes the number of combinations for a given n and r. It correctly models selection without repetition and provides a clear illustration of how combinatorial math can be translated into code.
The example shown here emphasizes clarity and correctness, making it ideal for students learning both Java math algorithms and basic combinatorics.
Java Code for Computing Combinations
Writing up an algorithm in Java to carry out the different Combination - Selection without Repetition, nCr - of a set of things requires some level of imaginative thinking.
Get a writing pad and pencil:
- Write out all n members in the set - for Combination - at the top of the pad.
- Beginning with the first member, match it separately with the other members until the required selected-group size (r) is reached.
-
When every possible Combination for this first member is
exhausted, remove the current first member from the mother set.
The immediate next member becomes the new first member in the culminating set. - Take the first member in what is left of the mother set and repeat the same process from step II.
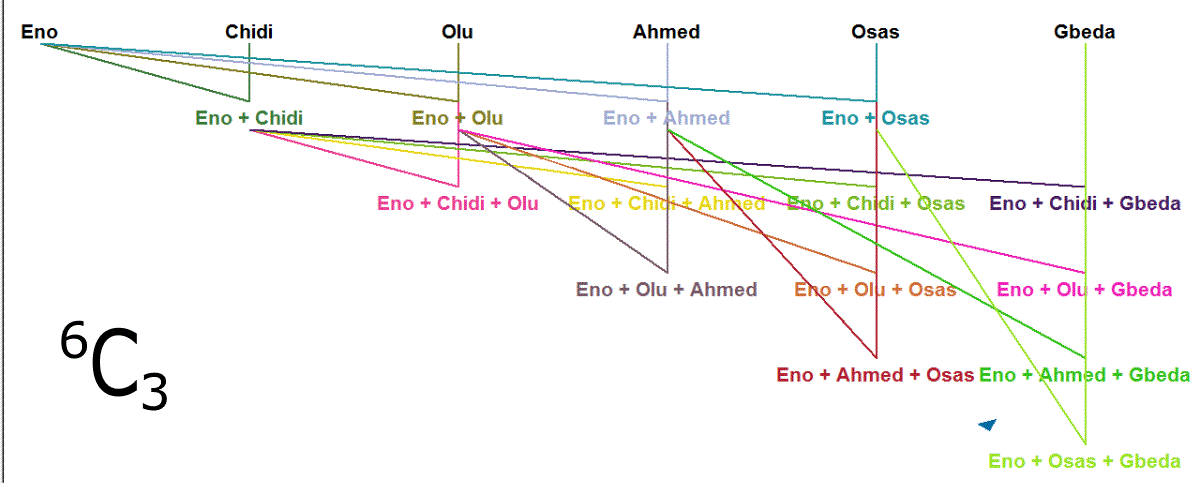
This is exactly what we will do with code to list up all
possible selections without repetition in Java.
Create a new Java project;
call it Miscellaneous
.
Create a new java class file;
call it Combination
.
Type out the adjoining Java code for the combination of different options
(\(^nC_r\)).
Why Combinations Matter in Programming | Explanation for Java Kids
Combination algorithms play an important role in many real-world programming scenarios. They help developers:
- Calculate possible outcomes efficiently
- Model real-life probability situations
- Apply mathematical reasoning to software solutions
Learning how to compute combinations in Java bridges the gap between theoretical mathematics and practical programming, reinforcing both disciplines simultaneously.
Practical Applications | Explanation for Java Kids
- Student group selection
- Lottery number generation
- Word combinations in Java
- Algorithm practice problems for beginners
Summary: Java Combination Algorithm
By understanding and implementing the Java combination algorithm, you can solve a wide range of problems in mathematics and programming. Whether you're calculating \(^nC_r\) in Java, generating all possible selections, or comparing combination vs permutation in Java, these techniques are essential for developers and learners alike.
This tutorial demonstrated how to:
- Understand combinations and the \(^nC_r\) formula
- Apply combinatorics concepts in Java
- Implement a clear combination algorithm for selection without repetition
By mastering these ideas, learners gain a solid foundation in both mathematical reasoning and Java algorithm development.
Java Code for Combination - Class File
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class Combination {
public List<String> words;
public int r; // min length of word
protected List<String[]> comb_store;
private int i;
public Combination() {
}
// point of entry
public List<String[]> possibleWordCombinations(List<String> candidates, int size) {
words = candidates;
r = size;
comb_store = new ArrayList<>();
i = 0;
// check for conformity
if (r <= 0 || r > words.size()) {
comb_store = new ArrayList<>();
} else if (r == 1) {
for (; i < words.size(); i++) {
comb_store.add(new String[]{words.get(i)});
}
} else {
progressiveCombination();
}
return comb_store;
}
// do combinations for all 'words' element
private void progressiveCombination() {
// single member list
repetitivePairing(Arrays.asList(words.get(i)), i + 1);
if (i + r <= words.size()) {
// move on to next degree
i++;
progressiveCombination();
}
}
// do all possible combinations for 1st element of this array
private void repetitivePairing(List<String> prefix, int position) {
List<String>[] auxiliary_store = new List[words.size() - position];
for (int j = 0; position < words.size(); position++, j++) {
// check if desired -- r -- size will be realised
if (r - prefix.size() <= words.size() - position) {
auxiliary_store[j] = new ArrayList<>();
auxiliary_store[j].addAll(prefix);
auxiliary_store[j].add(words.get(position));
if (auxiliary_store[j].size() < r) {
// see to adding next word on
repetitivePairing(auxiliary_store[j], position + 1);
} else {
comb_store.add(auxiliary_store[j].toArray(new String[0]));
}
}
}
}
}
Java Code for Combination - Main Class
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class Miscellaneous {
public static void main(String[] args) {
List<String> goods = new ArrayList<>();
goods.add("Eno");
goods.add("Chidi");
goods.add("Olu");
goods.add("Ahmed");
goods.add("Osas");
goods.add("Gbeda");
Combination combo = new Combination();
List<String[]> result = combo.possibleWordCombinations(goods, 4);
System.out.println(combo.words + " combination " + combo.r + ":\n");
int i = 0;
for (String[] set : result) {
System.out.println(++i + ": " + Arrays.toString(set) + ";");
}
System.out.println("\nNumber of ways is " + result.size() + ".");
}
}